오늘은 유니티에서 지난시간에 공부해본 삼각함수를 바탕으로 유니티에서 사용해보려합니다.
how?
우리가 알고있는 삼각함수를 어떻게 게임 개발에 사용할수있을까요?
이 사용방법을 알기위해 지난 시간에 배운 단위원을 다시한번 꺼내보겠습니다.

위 원은 반지름이 1인 기준의 단위원입니다.
우리가 빗변이 1인 직각삼각형의 경우 밑변의 길이가 즉 cos이고
높이의 길이가 sin이란것을 알수있었습니다.
여기서 중요한점은 원의 중심점에서부터
직각 삼각형의 높이의 해당하는 꼭지점까지의 좌표를 P라고 명칭하면
점의 중심점으로부터 P의 떨어져있는 좌표는 (밑변,높이)가 됩니다 이뜻은 (cos,sin)가 P의 좌표입니다.
여기서 피타고라스 정리를 착각하시고 혼란스러워 하시면 안됩니다.
피타고라스 정리로 알수있는건 원의 중심점으로부터의 P의 distance(거리)입니다.
우리가 구하고자 하는건 원의 중심점이 (0,0)일 경우 중심점 부터의 좌표(cos,sin) P라는겁니다.
이용해서 우리는 게임에서 특정 오브젝트를 원하는 각도로 이동이 가능해집니다.
예시
예를들어 원의 중심점에 플레이어가 있고 플레이어를 45도 방향으로 직진하게 만들고싶다.
(cos * 45,sin * 45)
계산하면 플레이어를 원하는 좌표로 이동할수있게됩니다.
여기서 중요한건 얼마만큼 가는가?
이 기준은 우리는 현제 단위원을 사용해서 빗변의 길이를 1로 가정해서 계산한 공식이기에
아직 길이의 정의가 없습니다
원하는 길이가 있다면 조금만 위 수식에서 추가만 해주면 됩니다.
플레이어를 45도 방향으로 4길이만큼 직진하게 만들고 싶다.
(cos * 45,sin * 45) * 4
끝입니다.
이로써 우리는 총알이나 모든 각도를 계산해야하는 오브젝트를 컨트롤할수있는
게임 개발 스킬이 늘었습니다.
자 지금까지 한 설명들이 제대로 동작하는지 유니티에서 실습을 통해서 확인해보겠습니다.
언리얼에서 실습을 할지 고민했지만 좌표계 기준이 보기편한 유니티로 기준했습니다.
유니티 실습

제가 사용하는 유니티 버전은 2022.3.5f1이며
다른 유니티 버전에서 실습을 따라 하셔도 크게 문제는 없을거라 생각합니다.
1. Sprite 오브젝트 player 생성
2. 스크립트 MoveController 생성
3. player에 방금 생성한 MoveController 컴포넌트 추가.
우리는 지금부터 player 객체를 원하는 각도로 이동하게 만드는 컴포넌트 MoveController를
방금 배운 수식을 이용해서 작성해보겠습니다.
4. MoveController 스크립트 더블 클릭
5. 밑 코드 복사 붙여 넣기
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class MoveController : MonoBehaviour
{
[Header("Angle")]
//theta
[SerializeField]
float deg_Angle;
[Header("Speed")]
[SerializeField]
float speed;
// Update is called once per frame
void Update()
{
var rad_Angle = DegreesToRadians(deg_Angle);
Vector2 duration = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));
transform.Translate(duration * speed *Time.deltaTime);
if (Input.GetKeyDown(KeyCode.R))
{
transform.position = new Vector2(0f, 0f);
}
}
private float DegreesToRadians(float _angle)
{
return _angle * Mathf.Deg2Rad;
}
}
6. ctrl + S 저장하고 유니티 에디터로 나갑니다.

MoveController 컴포넌트 사용법
코드를 설명하기 이전 우리가 원했던 목표대로 각도의 방향으로 정상 동작하는지 결과를 먼저 확인해보겠습니다.
빨간색 상자
실습에서 원하는 각도를 넣어서 정상적으로 이동하는지 확인해보실수있습니다.
노란색 상자
유니티 라이프 주기 업데이트문은 프레임과 다음 프레임을 불러오는 시간을 반환합니다.
각자 프로젝트 유니티 셋팅 환경에 따라 이 프레임수가 반환하게끔 셋업 되어있습니다.
각기다른 환경을 여러분에게 맞춰 간편하게 속도로 조절하기위해 speed라는 변수를 표현했습니다.
R키 버튼
R키를 누르면 플레이어의 좌표는 0,0으로 리셋됩니다.
영상 실습을 보며 유니티에서 각도의 기준을 같이 설명드리겠습니다.
영상 초기에 보시면 제가 Angle변수를 0으로 두고 이동 하는 경우
Transform Position이 x축만이 증가하고 y,z는 그대로인것을 확인할수있습니다.
유니티에서의 각도 기준은 우측 상단 1사분면부터 시작하는것을 우리는 확인할수있습니다.
또는 90으로 각도를 수정하면 Tranform이 x축의 변화없이 Y축만이 증가하는것으로
우리가 원하는 방향의 각도 조절을 삼각함수를 통해서 컨트롤할수있는것까지 확인했습니다.
자! 결과가 쉽게 나왔군요
너무 쉽게 결과가 나와서 더이상의 글이 필요가 없을것같습니다
이제 제가 만든 스크립트의 설명을 이어서 진행해보겠습니다.
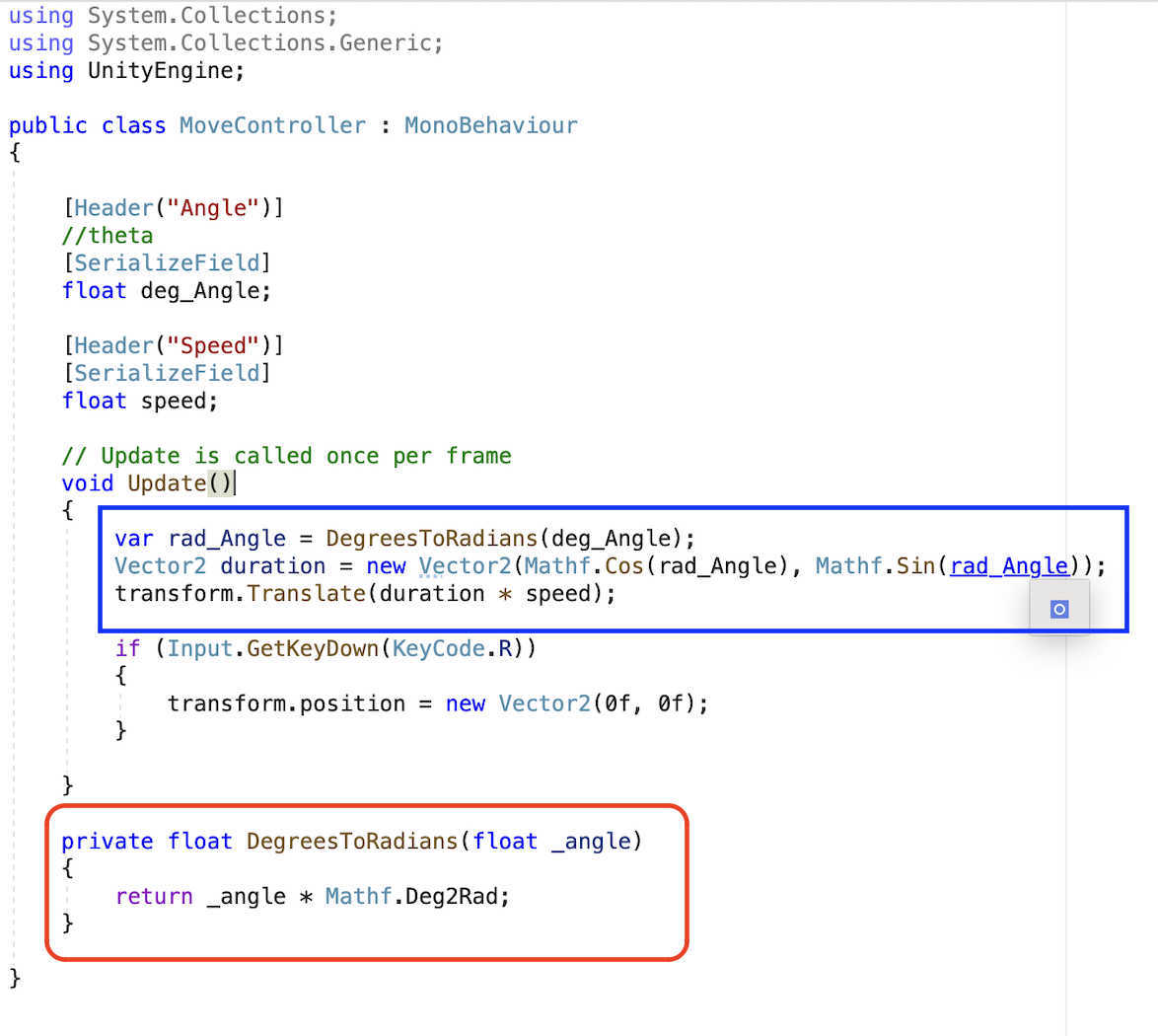
우리가 실습하려고 했던 공식 (cos * 각도, sin *각도)
이를 설명하기 기전 유니티에서는 조금 혼란스러운 삼각함수 사용법이 있습니다
유니티 mathf cos,sin은 라디안법을 사용하고 디그리를 사용하지 않습니다.

무슨뜻이냐면
우리가 0도, 90도 이런식의 각도 표현을 디그리법이라합니다
그리고 파이를 180이라 기준하고 파이 기준으로 나누거나 곱해서 각도를 표현하는 라디안법이란게 존재합니다.
유니티에서 사용되는 삼각함수는 라디안법을 매개변수로 필요로 하기에 우리는
디그리를 라디안으로 변환하는 과정을 거쳐야 합니다.
그것을 좀더 여러분이 복잡하지 않게 코드로 확인하실수있게끔 함수화하여 표현했습니다.
위 코드 이미지의 빨간색 함수가 디그리를 라디안으로 케스팅하는 과정입니다.
디그리를 라디안으로 바꾸는법은 간단하면서도 귀찮습니다
디그리 : 180/π 를 곱하면 라디안값이 나옵니다.
다행이 친절한 유니티는 deg2rad를 지원해줍니다.
유니티(Unity) 게임 엔진에서 Mathf.Deg2Rad는 디그리(Degree) 값을 라디안(Radian) 값으로 변환해주는 상수입니다.
디그리에서 라디안으로 변환할 때 사용되며, Mathf.Deg2Rad를 사용하면 간단하게 디그리 값을 라디안 값으로 변환할 수 있습니다.
우리는 그저 Deg2Rad에 디그리 각도를 곱해주면 라디안각도를 쉽게 구할수있습니다.
한줄짜리 함수이고 저렇게 쓰는방식을 저는 선호하지않습니다.
불필요한 뎁스가 많아지죠.
지금은 그저 여러분에게 코드에 대한 설명을 위해 캐스팅과정을 함수로 분리시킨것 뿐입니다.
이렇게 캐스팅 된 라디안법의 각도는 업데이트문 rad_Angle 변수에 저장됩니다.
우리가 원하는 수식이 바로 등장합니다.
벡터 변수를 보시면 지난글에서 지금까지 몇번이고 언급한 그 수식이 코드로 등장합니다
(cos * 이동시킬 변수),(sin * 이동시킬 변수)
좌표를 표현하기위해서 벡터를 선언하고 Mathf에서 지원하는 삼각함수를 사용합니다.
사용법은 안에 매개변수에 방금 캐스팅한 라디안 각도를 넣어서 사용합니다.
Vector2 duration = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));완성된 좌표값을 duration 벡터변수에 저장하면 우리가 원하고자하는 방향이 완성되었습니다
이를 지속적으로 이동시켜주는 함수 Translate에 사용하여 원하는 방향을 가지고 이동할수 있게됩니다.
원하는 각도를 구하는것만이 우리가 게임개발에 사용할수있는 삼각함수의 끝일까요?
지금 우리가 한 실습을 좀더 다양하게 응용하면 무한하게 활용할 방법이 존재합니다.
새로운 예시를 완성된 코드로 보여드리겠습니다.
삼각함수 유니티 원운동
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class MoveController : MonoBehaviour
{
[Header("Angle")]
//theta
[SerializeField]
float deg_Angle;
[SerializeField]
float speed;
[Header("Cricle")]
[SerializeField]
int i = 0;
[SerializeField]
int radius;
void Update()
{
//MoveAngle(deg_Angle);
}
private void FixedUpdate()
{
MoveCircle(radius);
}
private void LateUpdate()
{
if (Input.GetKeyDown(KeyCode.R))
{
transform.position = new Vector2(0f, 0f);
}
}
private void MoveAngle(float _deg_Angle)
{
var rad_Angle = DegreesToRadians(_deg_Angle);
Vector2 duration = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));
transform.Translate(duration * speed * Time.deltaTime);
}
private void MoveCircle(float _radius)
{
var rad_Angle = DegreesToRadians(i);
Vector2 direction = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));
direction *= _radius;
transform.Translate(direction * Time.fixedDeltaTime);
i++;
i = i > 360 ? 0 : i;
}
private float DegreesToRadians(float _angle)
{
return _angle * Mathf.Deg2Rad;
}
}
방금까지 실습한 원하는 각도로 이동하는 코드를 함수로 분리하고
다음 실습할 MoveCircle함수를 생성하였습니다.
MoveCircle함수의 역할은 우리가 이전에 실습한 각도이동을 응용하여 원으로 이동하는 원운동 함수를 만들어볼 계획입니다.
우선 코드의 설명에 앞서 미리 코드를 작성하고 실습영상으로 정상적으로 동작하는지 확인해보겠습니다.
1. 정수 변수 i 선언.
2. MoveCircle 함수 작성
3. FixedUpdate문 함수 호출
실습영상
영상에서 미리 결과를 확인해보면 정상적으로 원으로 이동하는 Player를 확인할수있습니다.
이 원들이 다양하고 많게 그리고 속도값을 추가하여 만들어내면
멋진 2D 행성 주기를 게임식으로 표현할수도 있겠네요
실습이 정상적으로 동작하는지 확인이 끝나셨다면 코드의 설명을 이어 진행해보겠습니다
i변수의 역할
i는 0~360을 반복하며 원을 그릴 각도를 무수히 반복하는 이동 각도입니다.
0~360까지 1씩 증가하는 값으로 원을 그리며 이동이 가능해집니다.
raidus 변수 역할
radius는 원의 크기 입니다.
raidus의 필요성은 단위원이라 보면됩니다.
각도를 구하는 공식 자체는 (cos * 각도 , sin * 각도) 입니다.
이 공식이 성립되는 조건은 단위원 빗변이 1이라는 전재조건이 있었기 때문이죠
1이 단위원의 기준이었다면 원의 반지름 빗변의 길이를 raidus변수로 지정하여
단위원의 기준으로 삼기위해 곱해줍니다.
Why FixedUpdate문을 사용했는가
FixedUpdate를 사용한 이유는 이전 직선운동의 경우는 프레임간의 호출값이 정확하지않은
time.deltime을 사용해도 우리가 원하는 경로의 이동에서는 문제가 없습니다.
하지만 원을 그리는 운동에서는 정확한 주기의 값을 원하기 때문에 fixedUpdate를 사용했습니다.
update문을 사용할경우 원의 중심점이 흐트러지며 정확한 원을 그리지 못합니다.
지금 배운 원을 그리는 운동은 단순한게 아닙니다.
실제 게임 로직에서 다양하게 쓰이는 기능의 구조입니다.
플레이어 전방기준 0~45도 사이 범위에 일정한 간격을 두고 투사체를 발사하라.

1945 핵엔슬래쉬 로그라이크 등 다양한 게임의 스킬에서 찾아볼수있는 기능입니다.
이전에서는 알수없었지만 지금에서는 우리는 볼수있습니다.
위 스킬 예시의 스킬을 유니티 삼각함수의 최종 마무리로 시작해보겠습니다.
불렛 프리펩 및 스크립트 작성

먼저 발사체 총알을 만들어보겠습니다.
1. 스프라이트 객체를 새 오브젝트로 생성
2. 이름은 bullet 총알같은 모양을 위해 스케일을 1,0.1,1로 설정
3. 리지드 바디2d 컴포넌트추가
4. 신규 스크립트 bullet을 만들고 컴포넌트를 추가
5. 리지드바디 중력값을 0으로 설정
6. 하단 프로젝트로 드래그앤 드랍해서 프리팹화
7. 하이어아키 불렛을 삭제
불렛의 코드는 짧기에 설명을 같이 진행하겠습니다.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Bullet : MonoBehaviour
{
public Rigidbody2D rb2d;
public float power;
private void Start()
{
rb2d = GetComponent<Rigidbody2D>();
rb2d.velocity = rb2d.transform.right * power;
}
}1. 멤버 변수 리지드바디2d, 물체의 힘을 가하기위해 실수 power 변수 선언
2. 라이프 주기 처음 단계인 start에 rb2d 레퍼런스를 정의
3. rb2d 속력 기준은 right로 지정
4. 유니티 에디터로 불렛프리펩의 power 값을 여러분이 원하는 속도로 지정합니다.
여기서 주목해야하는건 3의 불렛 속력기준을 transform.right로 기준한다는점입니다.
이는 플레이어의 moveController에서도 동일하게 오른쪽으로 기준할것이고
왜 오른쪽으로 기준하는가의 이유는
유니티의 각도 시작점의 기준이 우측 방향이기 때문입니다.
MoveController 클래스 제작
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class MoveController : MonoBehaviour
{
[Header("Angle")]
//theta
[SerializeField]
float deg_Angle;
[SerializeField]
float speed;
[Header("Cricle")]
[SerializeField]
int iter = 0;
[SerializeField]
int radius;
[Header("Skill")]
[SerializeField]
GameObject bulletPrefab;
[SerializeField]
Transform bulletHolder;
[SerializeField]
int interval;
[SerializeField]
int start_deg_Angle;
[SerializeField]
int end_deg_Angle;
void Update()
{
//MoveAngle(deg_Angle);
if(Input.GetKeyDown(KeyCode.K))
{
VolleyShot();
}
}
private void FixedUpdate()
{
MoveCircle(radius);
}
private void LateUpdate()
{
if (Input.GetKeyDown(KeyCode.R))
{
transform.position = new Vector2(0f, 0f);
}
}
private void MoveAngle(float _deg_Angle)
{
var rad_Angle = DegreesToRadians(_deg_Angle);
Vector2 duration = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));
transform.Translate(duration * speed * Time.deltaTime);
}
private void MoveCircle(float _radius)
{
var rad_Angle = DegreesToRadians(iter);
Vector2 direction = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));
direction *= _radius;
transform.Translate(direction * Time.fixedDeltaTime);
iter++;
iter = iter > 360 ? 0 : iter;
}
private void VolleyShot()
{
for(int i = start_deg_Angle; i < end_deg_Angle; i += interval)
{
var bullet = Instantiate(bulletPrefab, bulletHolder);
var rad_Angle = DegreesToRadians(i);
Vector2 direction = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));
bullet.transform.position = direction;
bullet.name = $"butllet_{i}";
bullet.transform.right = direction;
}
}
private float DegreesToRadians(float _angle)
{
return _angle * Mathf.Deg2Rad;
}
}코드의 설명은 실습 예제가 완성된 이후 진행하겠습니다.
위 코드를 복사 또는 직접 타이핑해서 설정해주시면됩니다.
MoveController prameter 셋업

위 코드가 완성되었다면 추가된 파라미터를 셋업하겠습니다.
1. 하이어아키 빈 오브젝트 생성 이름을 bulletHolder로 지정
2. 플레이어를 클릭하고 컴포넌트의 불렛프리펩에 이전에 만든 불렛으로 설정
3. bulletHolder를 1.에서 만든 빈객체를 드래그앤드랍해서 설정
4. 시작지점의 각도를 45도, 끝나는 부체꼴의 각도를 135도로 지정
5. 총알이 생성되는 간격을 15도로 지정.
6. 유니티 에디터로 나와서 플레이 버튼을 누르고 k 버튼을 클릭 발사체 동작하는지 확인
스킬영상
결과는 만족스럽에 동작하는것을 확인할수있습니다
사실 삼각함수를 쓰지않고도 물론 다양한 방법으로 위 로직을 구현할수 있습니다.
하지만 로테이션이나 오일러를 이용하는 구조는 더욱 코드가 어렵거나 손쉬운 컨트롤이 복잡하게 구현될 가능성이 높다고 저는 생각합니다.
위 단 한가지 기능으로 로그라이크류 게임의 보스몹 패턴을 다양하게 구현할수있습니다.
스킬 함수 설명
private void VolleyShot()
{
for(int i = start_deg_Angle; i < end_deg_Angle; i += interval)
{
var bullet = Instantiate(bulletPrefab, bulletHolder);
var rad_Angle = DegreesToRadians(i);
Vector2 direction = new Vector2(Mathf.Cos(rad_Angle), Mathf.Sin(rad_Angle));
bullet.transform.position = direction;
bullet.name = $"butllet_{i}";
bullet.transform.right = direction;
}
}
제가 여기서 설명드리고싶은 라인은
bullet.tranform.right를 direction 방향으로 초기화했다는점입니다.
나머지 코드는 방금 우리가 계속 반복적으로 가져온 기능을 그래도 가져왔을 뿐입니다.
새로 생성된 총알에 right의 방향이유는 불렛과 같습니다 유니티의 방향각도의 시작점이
x축이 0으로 기준이기때문입니다.이미 불렛에서도 속력값의 기준을 right로 지정한것이 큰 이유이기도 합니다.
그리고 이상하지 않습니까? 우리는 rotation을 건들지도 않았지만 tranform.right를 셋업한것으로
총알의 방향이 달라졌습니다.
이 지금까지의 로직은 어려울게 없지만 위 tranform.right는 생소하게 보일수밖에 없을거라 생각합니다.
Why?
tranform.right는 방향벡터의 역할을 수행합니다.
여기서의 벡터는 변수 벡터가 아닌 수학적 벡터를 뜻하기 때문입니다.
그리고 우리는 수학적 의미의 벡터는 설명하지 않았기도 했습니다.
방향벡터를 지금은 간단하게 생각해주시면 좋겠습니다.
단위원의 빗변의 길이가 1로 기준되어있는것처럼
오브젝트마다 각 단위원을 가지고있고 우리는 이 오브젝트의 단위원의 x축 방향을 우리가원하는 방향으로 컨트롤했다.
오늘 배웠던것들을 정리해보자면
1. 디그리법, 라디안법의 존재
2. 유니티에서 디그리를 라디안으로 캐스팅하는법
3. 삼각수학을 이용해서 원하는 각도로 물체를 이동시키는 법
4. 삼각수학을 이용해서 물체를 원으로 이동시키는 법
5. 부체꼴 모양의 스킬을 만드는법
오늘 유니티를 이용하여 삼각함수를 이용해서 다양한 실습을 해볼수있었습니다.
필요성도 느끼고 하드코딩으로 구현하는 로직보다 유연성을 알수도 있었습니다.
하지만 벡터의 필요성도 가져가게 됩니다.
다음 시간에서는 수학적 벡터의 설명을 가져보겠습니다
글이 어색하거나 이상하면 지적 부탁드립니다 항상 피드백을 기다립니다
읽어주셔서 감사합니다
'수학' 카테고리의 다른 글
| CMake란? (0) | 2025.06.29 |
|---|---|
| 게임 삼각함수 왜 필수이고 반드시 알아야 하는가 (0) | 2023.08.29 |
| [게임 개발] 왜 게임개발에서 벡터를 알아야하는가 (0) | 2023.01.15 |

